In order to operate at high speed from the acceleration area, it is necessary to start at low speed from the start area and then accelerate. When stopping, you need to act in the reverse order: first perform braking, and only after entering the start area can you stop supplying control pulses. Otherwise, a loss of synchronism will occur and the rotor position will be lost. The use of acceleration and deceleration makes it possible to achieve significantly higher speeds - in industrial applications speeds in excess of 10,000 full steps per second are used. It should be noted that continuous operation of the stepper motor at high speed is not always acceptable due to heating of the rotor. However, high speed can be used briefly for positioning purposes.
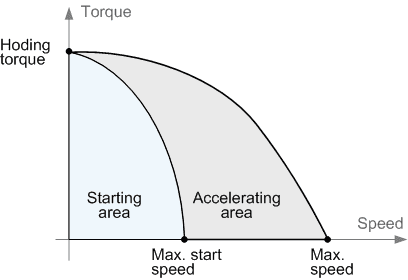
While accelerating, the stepper motor goes through a number of speeds, and at some of the speeds you such an unpleasant phenomenon as resonance may appear. For normal acceleration, it is desirable to have a load with moment of inertia value at least equal to the moment of inertia of the rotor. The resonance phenomenon is most pronounced for an unloaded motor.
When accelerating or braking, it is important to correctly select the law of speed change and maximum acceleration. The higher the load inertia, the lower the acceleration should be. The criterion for choosing the correct acceleration mode is to accelerate to the required speed for a specific load in the minimum time. In practice, acceleration and deceleration with constant acceleration are most often used.
The implementation of the law according to which the motor will be accelerated or decelerated is usually carried out by a software‑controlled microcontroller, since it is the microcontroller that is usually the source of the clock frequency for the stepper motor driver.
For the most general case, it is required to know the dependency of the step duration at the current speed. The number of steps the motor moves during acceleration in time t is:
N = 1/2 ∙ At2 + Vt,
N – number of steps,
t – time, sec,
V – speed, steps/sec,
A – acceleration, steps/sec2.
N = 1 for one step, so the speed duration is:
t1 = T = (-V + (V2 + 2A)0.5) / A
As a result, the speed becomes equal to Vnew:
Vnew = (V2 + 2A)0.5

